di Sergio Mauri
La R.O. è una disciplina scientifica recente; come definizioni di ricerca operativa, quella di R.L. Ackoff e M.W. Sasieni[1] sono chiare e sintetiche. Essa afferma che:
“La ricerca operativa può essere considerata l’applicazione del metodo scientifico, da parte di gruppi interdisciplinari a problemi che implicano il controllo di sistemi organizzati (uomo-macchina) al fine di fornire soluzioni che meglio servono gli scopi dell’organizzazione nel suo insieme”.
La ricerca operativa perciò fornisce soluzioni ottenute con metodi scientifici ai problemi aziendali, permettendo di effettuare scelte razionali. In virtù dei problemi che si presentano nella realtà, la ricerca deve essere multidisciplinare, affinché il problema sia esaminato sotto vari aspetti e, quindi, le soluzioni possano essere le più soddisfacenti in relazione all’obiettivo posto.
La R.O. si articola in diverse fasi:
- Approfondito esame della situazione e raccolta delle informazioni.
- Esposizione del problema, individuando le variabili controllabili (per esempio la quantità di beni prodotti) e quelle non controllabili (per esempio le variazioni della domanda) e la funzione economica da massimizzare (profitti o vendite) o da minimizzare (costi o perdite).
- Costruzione del modello matematico, cioè rappresentando il problema in modo che il modello si avvicini il più possibile alla realtà di interesse.
- Ricerca della soluzione del modello, cercando cioè di migliorare la soluzione attraverso metodi di iterazione e/o analisi numerica.
- Analisi e verifica delle soluzioni.
Rappresentazione diagrammatica delle fasi:
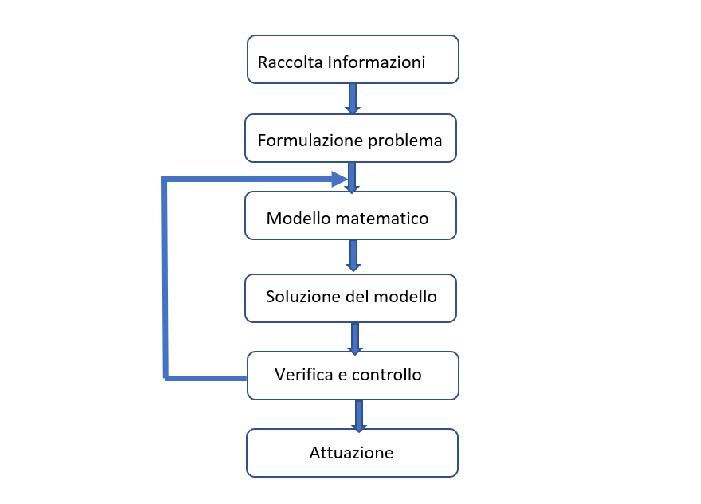
Alcuni problemi in cui è coinvolta direttamente la ricerca operativa, sono stati risolti in modo specifico attraverso:
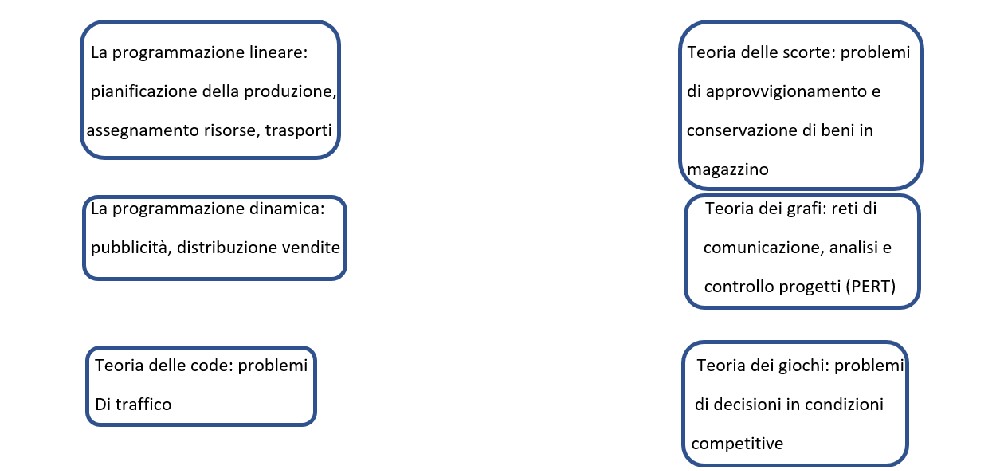
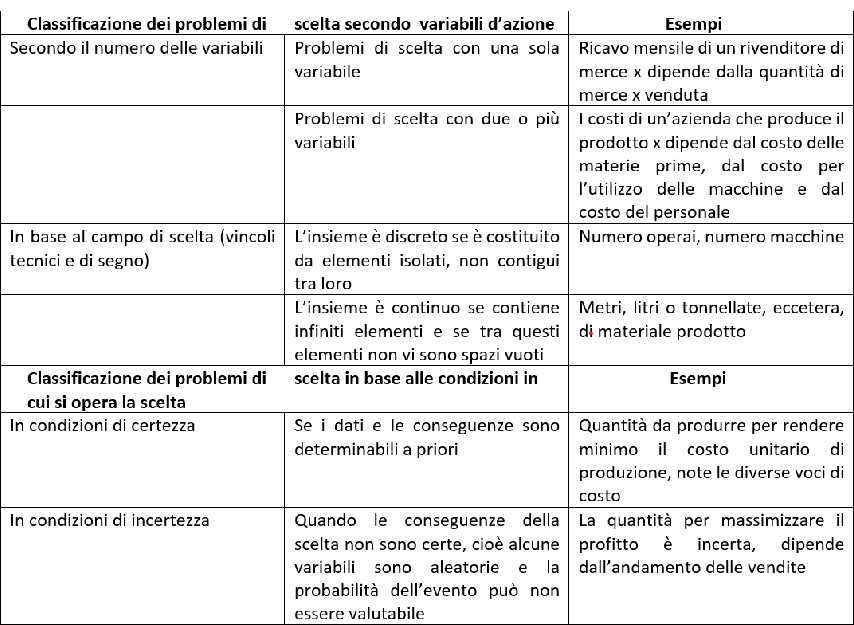

Analizziamo meglio queste distinzioni:
Problemi in condizioni di certezza: le grandezze che intervengono nel problema assumono valori certi e gli effetti della scelta sono noti.
Problemi in condizioni di incertezza: una o più grandezze del problema sono variabili casuali che assumono valori differenti in relazione al verificarsi o meno di certi eventi aleatori. Nemmeno gli effetti della scelta sono noti, ma dipendono dal verificarsi di quegli eventi. In questo caso per risolvere il problema usiamo il calcolo delle probabilità.
Problemi di scelta con effetti immediati: gli effetti economici si verificano immediatamente. Non vi è un lasso di tempo tra il sostenimento dei costi e l’ottenimento dei ricavi.
Problemi di scelta con effetti differiti: le conseguenze della scelta sono differite nel tempo, cioè decorre un periodo di tempo tra il momento del sostenimento dei costi e la realizzazione dei ricavi. In generale parliamo di problemi in ambito finanziario (scelta tra investimenti alternativi) o industriale (scelta tra due o più macchinari da acquistare, sulla base del costo, della durata, dei ricavi d’esercizio che da essi provengono, dai costi di manutenzione. Nel caso dell’eliminazione del macchinario, possiamo avvalerci della matematica finanziaria).
Problemi di tipo continuo: le variabili d’azione assumono un numero infinito di valori in un certo intervallo. Di conseguenza vi sono infinite possibilità.
Problemi di tipo discreto: le variabili d’azione possono assumere un numero finito di valori e quindi i risultati saranno in numero finito.
Vediamo in concreto ora i problemi di scelta in condizioni di certezza ad effetti immediati ad una variabile d’azione.
Essi sono: problemi di massimizzazione del guadagno (Break Even Point e diagramma di redditività); problemi di minimizzazione del costo unitario; problema delle scorte; altri problemi di tipo discreto; problemi di scelta tra più alternative.
In questi problemi la F.O. (il guadagno) può essere una funzione lineare (retta), una parabola, un’iperbole, una funzione definita a tratti. Si cerca di attribuire un valore alla variabile d’azione (quantità da produrre) affinché il valore della F.O. sia massimo. In questo caso il modello matematico è:
GUADAGNO = RICAVO – COSTI
G(X) = R(X) – C(X)
Dove R(X) = p * x p= prezzo unitario di vendita fisso o variabile
X = quantità
C(X) = COSTI FISSI + COSTI VARIABILI
I costi fissi sono dei costi sostenuti dall’impresa a prescindere dalla quantità prodotta mentre i costi variabili dipendono dalla quantità prodotta, come ad esempio dal costo della materia prima.
Perciò: F.O. = guadagno
V.A. = quantità da produrre
Vincoli = vincolo di segno e limite della capacità produttiva
I problemi di decisione si possono classificare secondo varie caratteristiche, come segue:
[1] Teorici e docenti americani delle organizzazioni. Noti per il libro a quattro mani Fondamenti di ricerca operativa del 1972.